CTC (Connectionist Temporal Classification)
CTC
论文地址:http://people.idsia.ch/~santiago/papers/icml2006.pdf
1.背景
CTC本质上就是一个序列学习任务中使用到的encoder-decoder网络结构:
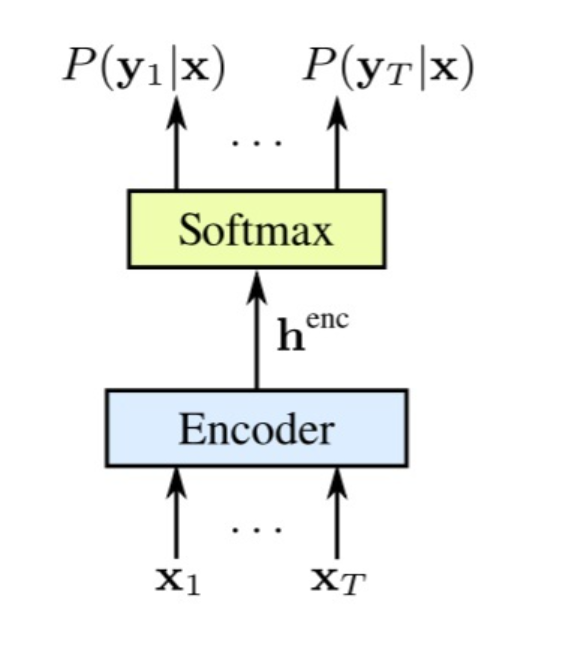
在序列学习任务中,模型对训练样本一般有这样的依赖条件:输入序列和输出序列之间的映射关系已经事先标注好了。比如,在词性标注任务中,训练样本中每个词(或短语)对应的词性会事先标注好,如下图(DT、NN等都是词性的标注链接)。由于输入序列和输出序列是一一对应的,所以模型的训练和预测都是端到端的,即可以根据输出序列和标注样本间的差异来直接定义模型的Loss函数,传统的RNN训练和预测方式可直接适用。
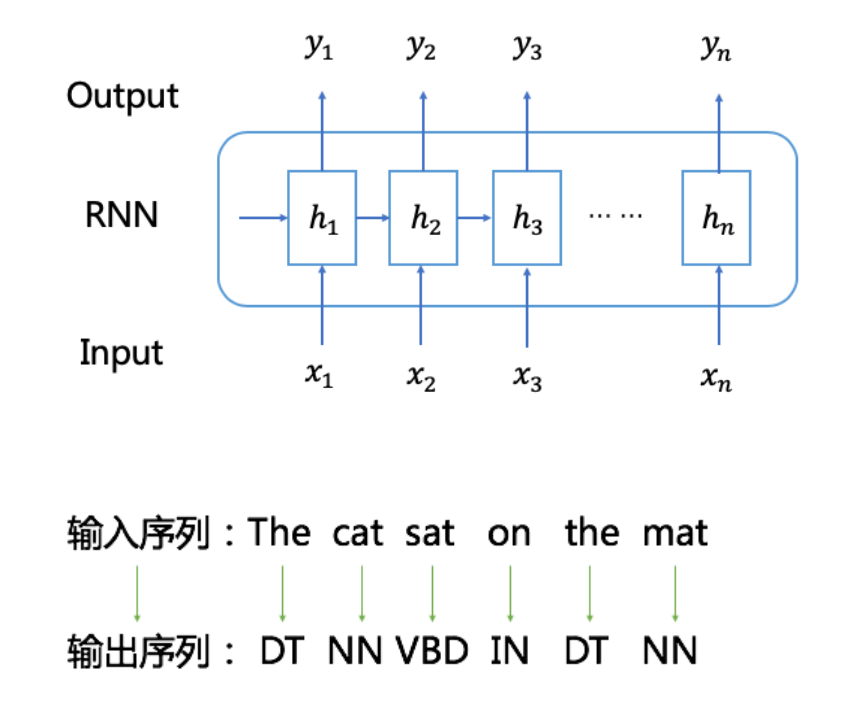
然而,在语音识别、手写字识别等任务中,由于音频数据和图像数据都是从现实世界中将模拟信号转为数字信号采集得到,这些数据天然就很难进行“分割”,这使得我们很难获取到包含输入序列和输出序列映射关系的大规模训练样本(人工标注成本巨高)。因此,在这种条件下,RNN无法直接进行端到端的训练和预测。
如下图,输入是“apple”对应的一段说话音频和手写字图片,从连续的音频信号和图像信号中逐一分割并标注出对应的输出序列非常费时费力,在大规模训练下这种数据要求是完全不切实际的。而如果输入序列和输出序列之间映射关系没有提前标注好,那传统的RNN训练方式就不能直接适用了,无法直接对音频数据和图像数据进行训练。
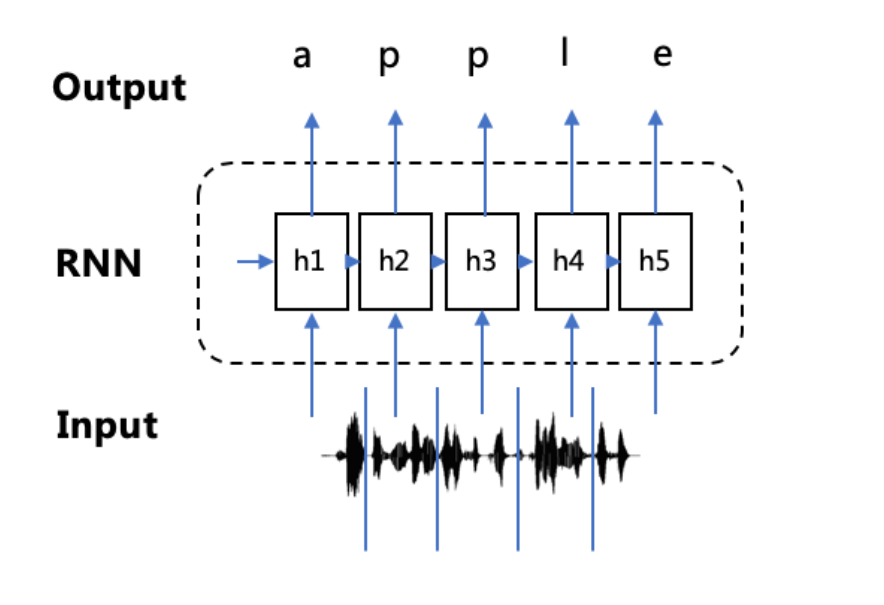
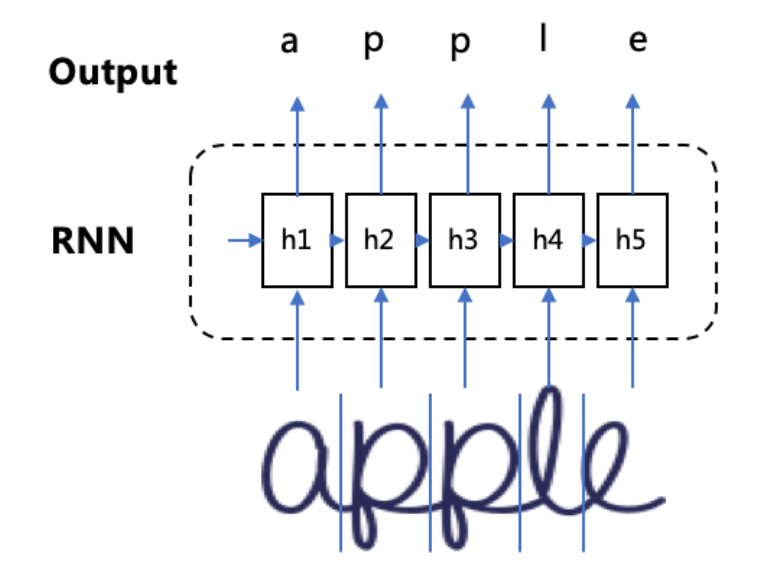
对音频“分割”并标注映射关系的数据依赖是不切实际的,实际情况是对音频按照时间窗口滑动来提取特征,例如按照每帧音频提取特征:
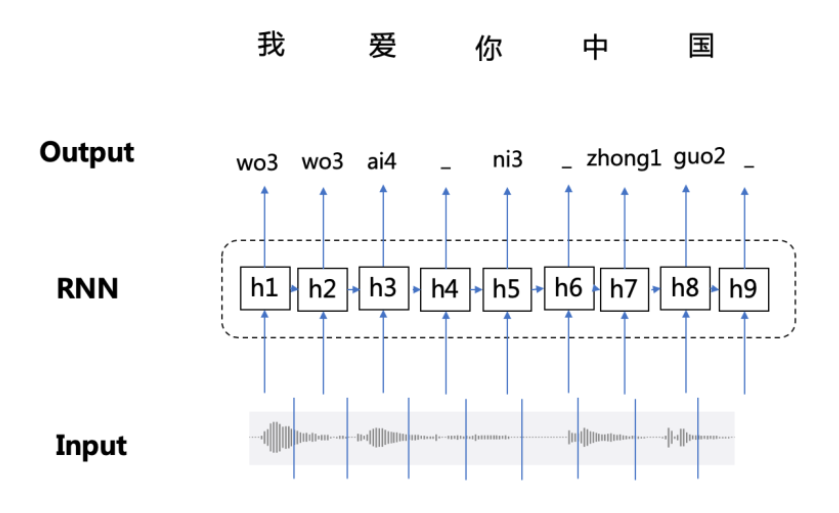
因此,在语音识别、手写数字识别等领域中,由于数据天然无法切割,且难以标注出输入和输出的序列映射关系,导致传统训练方法不能直接适用。那么,如何让RNN模型实现端到端的训练成为了关键问题。
Connectionist Temporal Classification(CTC)是Alex Graves等人在ICML 2006上提出的一种端到端的RNN训练方法,它可以让RNN直接对序列数据进行学习,而无需事先标注好训练数据中输入序列和输入序列的映射关系。
2.CTC算法
给定输入序列$X=[x_1,x_2,…,x_T]$ 以及对应的标签数据$Y=[y_1,y_2,…,y_U]$ ,如语音识别中的音频文件和文本文件。我们的目的是找到 $X$ 到 $Y$ 的一个映射函数
对比传统的分类方法,有如下难点:
- $X$ 和 $Y$ 的长度都是变化的且不相等的;
- 对于一个端到端的模型,我们并不希望手动设计$X$ 和 $Y$ 的之间的对齐。
2.1 对齐方式
CTC本身是不需要对齐的,但是我们需要知道 $X$ 的输出路径和最终输出结果的对应关系,因为在CTC中,多个输出路径可能对应一个输出结果。例如在语音识别的任务中,输入 $X$ 是“CAT”的语音,输出 $Y$ 是文本[C, A, T]。将 $X$ 分割成若干个语音帧,每一帧得到一个输出,一个最简单的解决方案是合并连续重复出现的字母:

直接这样对齐有两个缺点:
- 几乎不可能将 $X$的每个时间片都和输出Y对应上,例如OCR中字符的间隔,语音识别中的停顿;
- 不能处理有连续重复字符出现的情况,例如单词“HELLO”,按照上面的算法,输出的是“HELO”而非“HELLO”。
为了解决上面的问题,CTC引入了空白字符 $\epsilon$ ,例如OCR中的字符间距,语音识别中的停顿均表示为 $\epsilon$ 。所以,CTC的对齐涉及去除重复字母和去除 $\epsilon$ 两部分:

2.2 损失函数
对于给定的训练数据$(X,Y)$ ,本质上我们需要对$P(Y|X)$建模,但根据以上定义的对齐方式,多个输出路径均可能对应同一个输出结果$Y$
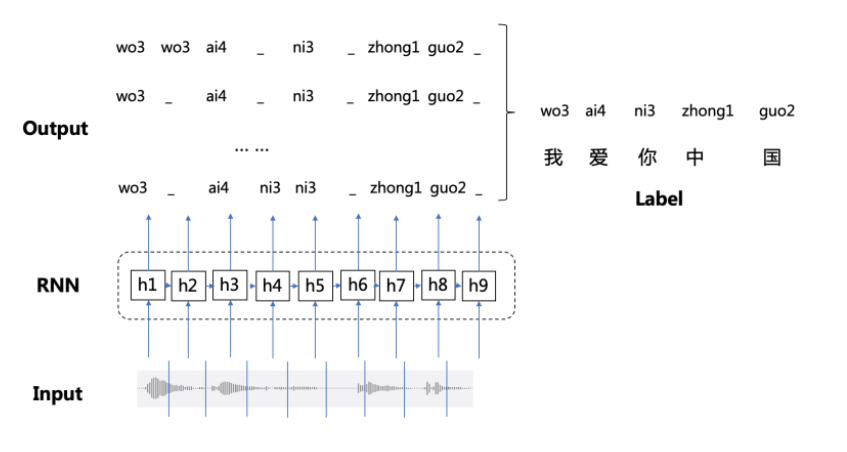
也就是说,对于标签 $Y$ ,其关于输入 $X$ 的后验概率可以表示为所有映射为 的$Y$路径之和,我们的目标就是最大化 $Y$ 关于 $X$ 的后验概率 。假设$P(Y|X)$每个时间片的输出是相互独立的,则路径的后验概率是每个时间片概率的累积
其中,$(X,Y)$ 分别表示输入及输出,$O$ 表示所有可能的对齐方式,$p_t(o_t|x_t)$ 表示在时刻t输出字符 $o_t$的概率.
因此,只需要穷举出所有的$O$ ,累加一起即可得到$P(Y|X)$,从而使得RNN模型对最终的label进行建模。
对于一个训练集合$S{(X,Y)}$ ,CTC的损失函数可定义为训练集S所有样本的负对数似然概率之和:
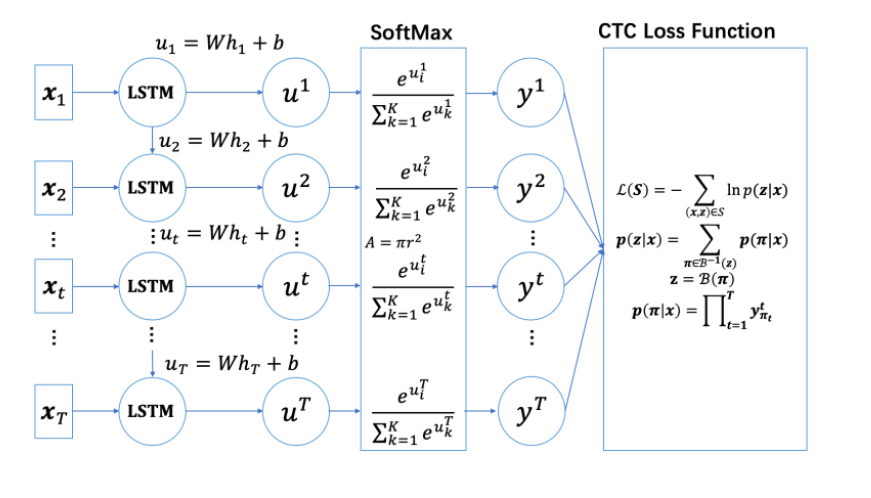
但这样的CTC算法存在性能问题,对于一个时间片长度为 $T$ 的 $N$ 分类任务,所有可能的路径数为 $T^N$ ,在很多情况下,用于计算Loss几乎是不现实的。在CTC中参照了HMM中的算法,采用了动态规划的思想来进行计算.
2.3 前后向概率及训练
为了更形象表示问题的搜索空间,将所有的路径放在坐标轴中,并把输出序列$Y=[y_1,y_2,…,y_U]$做标准化处理,输出序列中间和头尾都加上$\epsilon$,得到$Z=[\epsilon, y_1,\epsilon,y_2,…,y_U,\epsilon]$, 横轴的单位是$X$对应的时间步, 纵轴是标签$Y$插入$\epsilon$后的序列$Z$,例如:
以“ZOO”这个标签为例,按照时间步(T=9)展开,则可将$P(Y|X)$ 的所有可能的合法路径表示如下图:
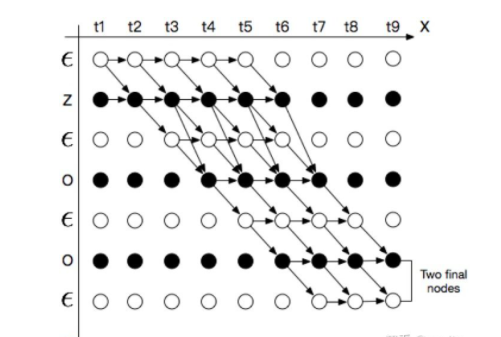
为了让所有的路径都能在图中有唯一且合法的表示,节点转换有一定约束。
接下来利用动态规划思想计算所有路径的概率总和:
定义在$t$时刻经过节点$s$的全部前缀子路径的概率总和为前向概率为 $\alpha_t(s)$,表示已经输出部分观察值$x_1,x_2,…,x_t$ 且$t$时刻输出标签为$s$ 的概率,用$p_t(z_s|x_t)$ 表示在$t$时刻输出字符$z_s$ 的概率
Case 1:
如果 $z_s=\epsilon$, 则 $\alpha_t(s)$ 只能由 $\alpha_{t-1}(s_{t-1})$ 或者 $\alpha_{t-1}(s)$ 得到,如果$z_s\ne\epsilon$ 但$z_s$为连续字符,即$z_s=z_{s-2}$,则 $\alpha_t(s)$ 也只能由 $\alpha_{t-1}(s-1)$ 或者 $\alpha_{t-1}(s)$ 得到,即:
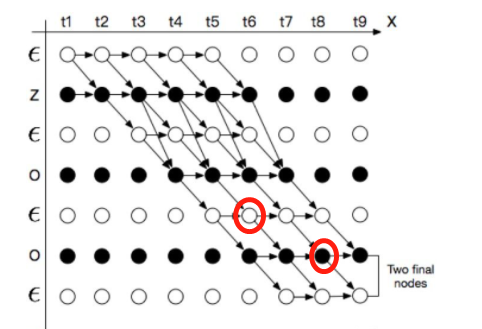
Case 2:
如果$z_s\ne\epsilon$ 且不为连续字符,则$\alpha_t(s)$ 可以由 $\alpha_{t-1}(s_{t-2})$ , $\alpha_{t-1}(s_{t-1})$ 以及 $\alpha_{t-1}(s)$ 得到,即:
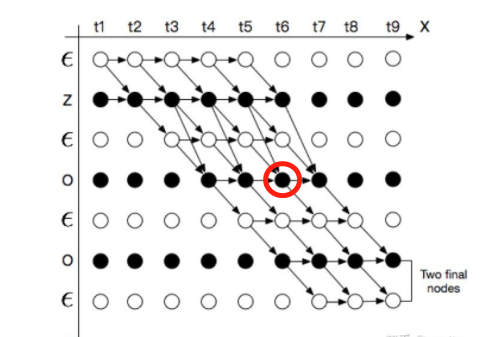
可得到CTC的前向概率递推计算:
同理,定义后向概率$\beta_t(s)$ 表示在$t$时刻输出标签为$s$ 及输出观察值序列为$x_t,x_{t+1},…,x_T$ 的概率,同样可得 CTC的后向概率计算:
利用前向概率和后向概率计算CTC的损失函数:
由此,即可用BPTT算法对CTC进行训练:
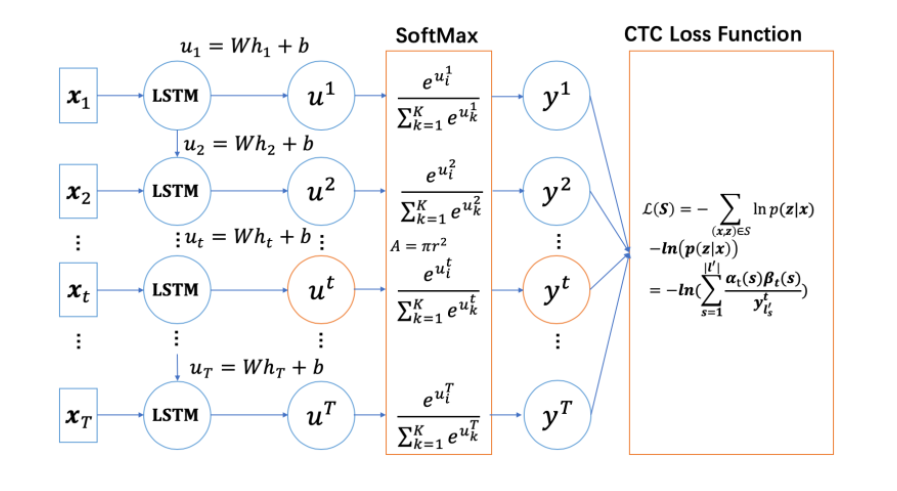
3. 解码
给定一个输入序列 $X$ ,我们需要找到最可能的输出:
Greedy Search: 每个时间片均取该时间片概率最高的节点作为输出
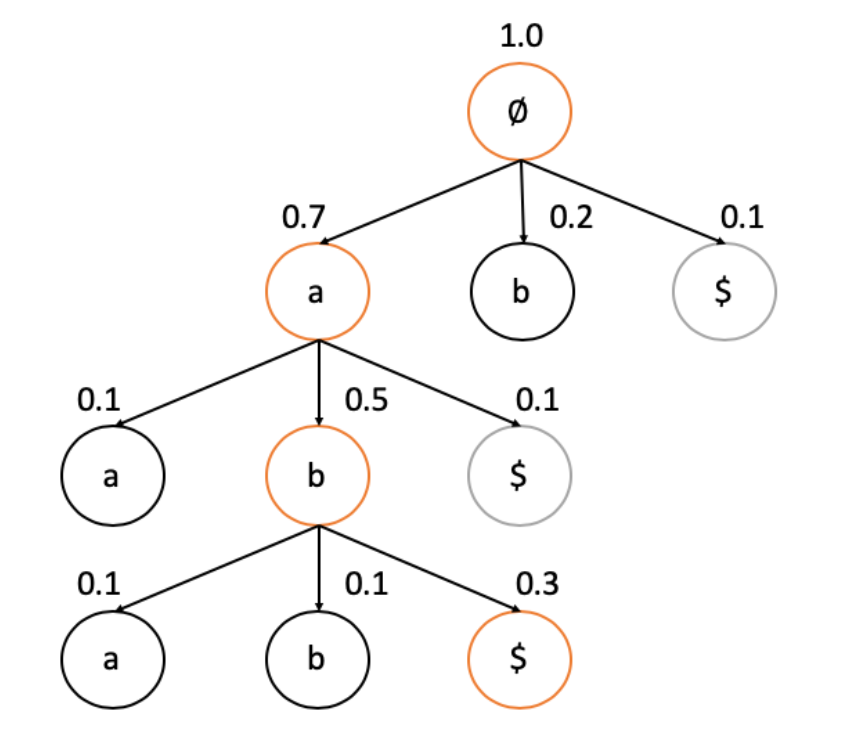
Beam search
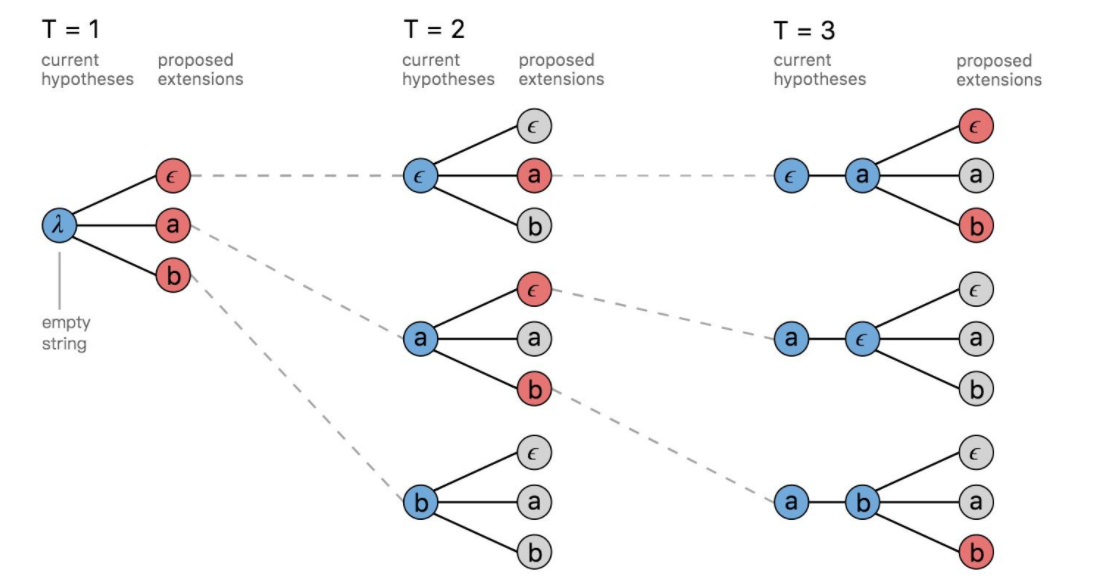
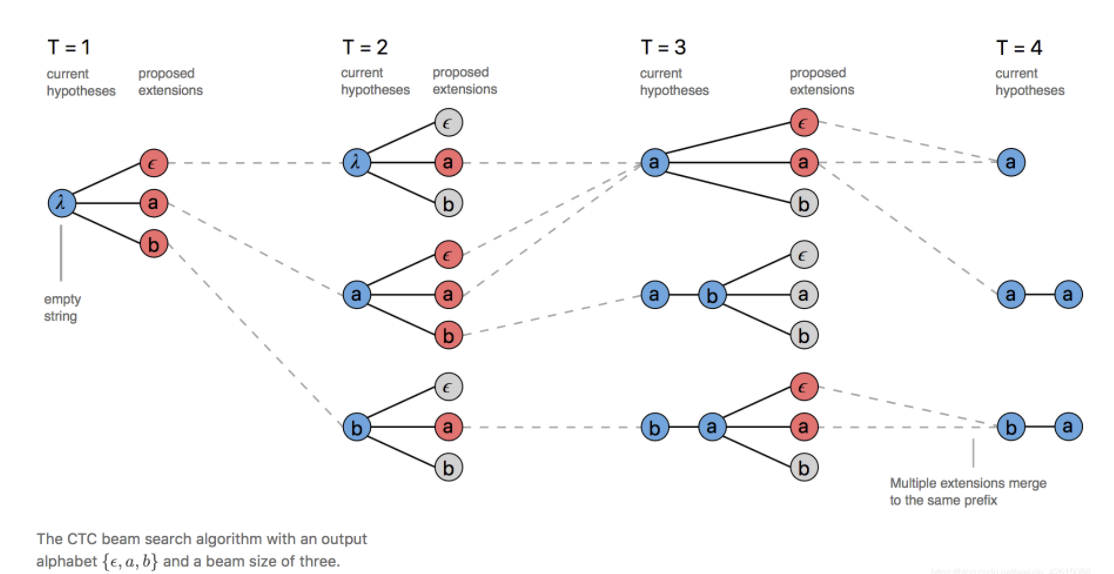
Prefix Beam Search
有许多不同的路径在many-to-one map的过程中是相同的,但beam search却会将一部分舍去,这导致了很多有用的信息被舍弃了,基本的思想是在搜索过程中不断的合并相同的前缀:
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!